The first thing we are going to do is arrange both equations so the variables will be in the left side, and the numbers in the right side.
For our first equation:
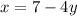
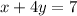
For our second equation:
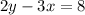
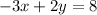
Now, we can rewrite our system of equations:

Next, we are going to express our system as a matrix equation. To do that we will create a coefficient matrix first, which is just the grid of the coefficients of our variables with brackets aground them; then we are going to multiply it by the column vector

,

, and then we are going to set all of that equal to the column vector 7, 8:
![\left[\begin{array}{ccc}1&4\\-3&2\end{array}\right] \left[\begin{array}{ccc}x\\y\\\end{array}\right] = \left[\begin{array}{ccc}7\\8\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/bs69oxvs6wxfsgthjst08qrgepeov8mjyv.png)
Now, we will apply Cramer's rule to solve our matrix equation:
First we are going to find the determinant of our coefficient matrix by multiplying a top to bottom and left to right diagonal and subtract from that a bottom to top and left to right diagonal:
![D= \left[\begin{array}{ccc}1&4\\-3&2\end{array}\right] =(1)(2)-(-3)(4)=2+12=14](https://img.qammunity.org/2019/formulas/mathematics/high-school/f6ngew355lw77gytulio8yp0hxvi5u85gd.png)
Next, we are going to find the determinant of

following the same procedure as before, but replacing the coefficients of

with the column vector 7, 8:
![D_(x)= \left[\begin{array}{ccc}7&4\\8&2\end{array}\right] =(7)(2)-(8)(4)=14-32=-18](https://img.qammunity.org/2019/formulas/mathematics/high-school/qwmkzaljcx9gu9l8patk6kz1e5yaemiyn3.png)
Next, we are going to find the determinant of

following the same procedure as before, but replacing the coefficients of

with the column vector 7, 8:
![D_(y)= \left[\begin{array}{ccc}1&7\\-3&8\end{array}\right] =(1)(8)-(-3)(7)=8+21=29](https://img.qammunity.org/2019/formulas/mathematics/high-school/sl6wnd71fuu57owyhbmkstnfayyk118f79.png)
Finally, we have all we need to use Cramer's rule and solve our system of equations:

and

Since we know that

,

, and
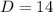
, lets replace those values in our Cramer's rule equations to find the values of

and

:

and

We can conclude that the solution of our system of equations is
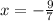
and

.