Answer:

Explanation:
You transcribed the equation incorrectly, but that's okay as I do know the correct volume formula. That is:
v = πr²h
In other words, the volume of a cylinder is simply the area of one of its circular ends, multiplied by its length. Now that we have that, let's solve for h:
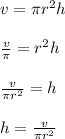
So the height of the cylinder can be calculated given the volume and the radius, simply by dividing the volume by pi times the square of its radius.