Answer:
Hence, perimeter of ΔAEB is:
18.5 ft.
Explanation:
The perimeter of ΔAEB is given as:
length of side AE+length of side BE+length of side AB.
As side AB║DF hence we will use Triangle Proportionality theorem to calculate the length of side AE.
Since,
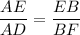
Hence, we have:
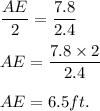
Hence, perimeter of ΔAEB is:
6.5+4.2+7.8=18.5 ft.
( since AE=6.5 ft
BE=7.8 ft
and AB=4.2 ft )
Hence, perimeter of ΔAEB is:
18.5 ft.