Question

The vertices of a triangle ABC are A(7, 5), B(4, 2), and C(9, 2). What is measure of angle ABC? 30° 45° 56.31° 78.69°

Answer 1

45

Explanation:

Answer 2

The measure of angle ABC is 45°

Explanation

Vertices of the triangle are: A(7, 5), B(4, 2), and C(9, 2)

According to the diagram below....

Length of the side BC (a)
`=√((4-9)^2+(2-2)^2)= √(25)= 5`

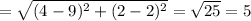
Length of the side AC (b)
`= √((7-9)^2 +(5-2)^2)= √(4+9)=√(13)`

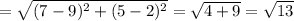
Length of the side AB (c)
`= √((7-4)^2 +(5-2)^2) =√(9+9)=√(18)`

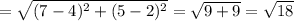
We need to find ∠ABC or ∠B . So using Cosine rule, we will get...

`cosB= (a^2+c^2-b^2)/(2ac) \\ \\ cos B= ((5)^2+(√(18))^2-(√(13))^2)/(2*5*√(18) )\\ \\ cosB= (25+18-13)/(10√(18)) =(30)/(10√(18))=(3)/(√(18))\\ \\ cosB=(3)/(3√(2)) =(1)/(√(2))\\ \\ B= cos^-^1((1)/(√(2)))= 45 degree`

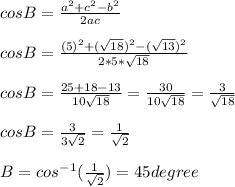
So, the measure of angle ABC is 45°