Question

How do you solve this? cosθ-tanθcosθ=0

Answer 1

First, lets note that
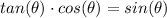
`tan(\theta)\cdot cos(\theta)=sin(\theta)`. This leads us with the following problem:


`cos(\theta)-sin(\theta)=0`

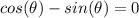
Lets add sin on both sides, and we get:


`cos(\theta)=sin(\theta)`

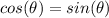
Now if we divide with sin on both sides we get:


`(cos(\theta))/(sin(\theta))=1`

Now we can remember how cot is defined, it is (cos/sin). So we have:


`cot(\theta)=1`

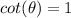
Now take the inverse of cot and we get:

`\theta=cot^(-1)(1)=\pi\cdot n+ (\pi)/(4) , \quad n\in \mathbb{Z}`

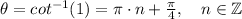
In general we have
`cot^(-1)(1)=(\pi)/(4)`, the reason we have to add pi times n, is because it is a function that has multiple answers, see the picture: