This includes 4 questions:
a) what is the probability that a US adult has a landline?
This can be tackled in many ways; the easiest is to add the percentages of the people that have landlines and cell phones and the number of people that have only landlines (they are mutually exclusive sets). Given the table, this yields:
29%+22+7%=58%
b) What is the probability that a US adult has a landline given that he has a cellphone?
The percentage of people that have cellphone can be calculated as above; 39% have only cellphones and 29% have both cellphones and a landline. Thus, in total 68% of the pouplation has cellphones. From this percentage, 29% has also a landline. Hence, the probability that a person that has a cellphone also has a landline is
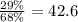
. (Intuitively, we restricted the domain to the people that have a cellphone and then did our calculations using only samples from that domain).
c)There is a simple check; if they are independent, the probability that a person has both is simply the product of the individual probabilities. THe probability for landline is 58%. The probability for cellphone is 68%. Thus their product is 39.4%. This is different from the probability that people have both a cellphone or a landline which is only 29%. Because 29<39, this means that if a person has a landline or a cellphone, he is likely than the average person to also have the 2nd means of communication. They are not independent.
d) For two events to be disjoint, it needs to be that they cannot happen in the same circumstance. More precisely, the sets of outcomes that they describe need to not have an overlap. For example, acourtain being blue and a courtain being red are disjoint events if courtains are only allowed to have one color. Another pair of disjoint events is negation pairs; for example Bill drinking his juice and Bill not drinking his juice. If the one happens, the other cannot happen. Here however, it is possible that an adult has both a landline and a cellphone (29%). Thus, these two events are not disjoint.