Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.

Find the missing part.

Answer 1

1) To find
`x` we are going to use the Pythagorean equation:

`x= \sqrt{a^(2)+b^(2) }`
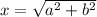
where

`a` and
`b` are the legs of our triangle. For our picture we can infer that
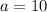
`a=10` and
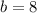
`b=8`, so lets replace those values in our equation to find
`x`:

`x= \sqrt{10^(2)+8^(2)}`

`x= √(100+64)`

`x= √(164)`

`x=12.8`
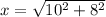
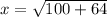
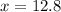
We can conclude that the value of
`x` in our triangle is 12.8

2) To find
`y` we are going to use the trigonometric function tangent. Remember that
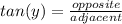
`tan(y)= (opposite)/(adjacent)`. We know that the opposite side of our angle
`y` is 8, and its adjacent side is 10, so lets replace those values in our tangent function to find
`y`:

`tan(y)= (8)/(10)`

`tan(y)=0.8`
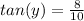
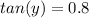
Since we need the measure of angle
`y`, we are going to take inverse tangent to both sides to find it:

`y=arctan(0.8)`

`y=38.66`
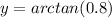
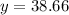
We can conclude that the value of
`y` in our triangle is 38.66°

3) Finally, to find
`z` we are going to take advantage of two facts: the sum of the interior angles of a triangle is always 180°, and our triangle is a right one, so one of its sides is 90°. Therefore,
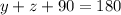
`y+z+90=180`. Since we already know the value of
`y`, lets replace it in our equation and solve for
`z`:

`38.66+z+90=180`

`z+128.66=180`

`z=51.34`
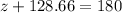
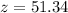
We can conclude that the measure of angle
`z` is 51.34°