Question

A (-1,5) B (0,6) D (0,2) Kite ABCD has the vertices shown. Find the coordinates of point C. A) (2, 5) B) (1, 5) C) (1, 4) D) (1, 6)

Answer 1

If ABCD is a kite, then by definition it has two pairs of congruent sides.

Let point C has coordinates (a,b).

Then

• 
  `AB=√((-1-0)^2+(5-6)^2)=√(1+1)=√(2);`
• 
  `BC=√((a-0)^2+(b-6)^2);`
• 
  `CD=√((a-0)^2+(b-2)^2);`
• 
  `AD=√((-1-0)^2+(5-2)^2)=√(1+9)=√(10).`

Solve the system of equations:

`\left\{\begin{array}{l}√((a-0)^2+(b-6)^2)=√(2)\\√((a-0)^2+(b-2)^2)=√(10)\end{array}\right.`

Square these two equations and then subtract:

`(b-6)^2-(b-2)^2=2-10,\\ \\b^2-12b+36-b^2+4b-4=-8,\\ \\-8b=-8-32,\\ \\-8b=-40,\\ \\b=5.`

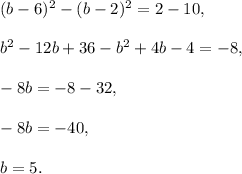
Substitute b=5 into the first equation:

`√(a^2+(5-6)^2)=√(2),\\ \\a^2=2-1,\\ \\a^2=1,\\ \\a=1 \text{ or } a=-1.`

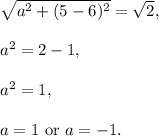
You get two points (1,5) and (-1,5). Point (-1,5) coincides with point A, so C(1,5).

Answer: correct choice is B.

Answer 2

B) (1, 5) is your best answer

B (0,6) creates the top of the kite
D (0,2) creates the bottom
A (-1,5) creates the left side of the kite
D (1,5) creates the right side (only the x is flipped, because has congruent sides of both the top, and both the bottom.

hope this helps