Question

Quadrilateral JKLM has vertex coordinates J(2,4), K(6,1), L(2,-2), and M(-2,1). What type of quadrilateral is JKLM?

Answer 1

Find lengths of quadrilateral sides:

`|JK|=√((6-2)^2+(1-4)^2) =√(16+9)=5`,

`|KL|=√((2-6)^2+(-2-1)^2) =√(16+9)=5`,

`|LM|=√((2-(-2))^2+(-2-1)^2) =√(16+9)=5`,

`|MJ|=√((-2-2)^2+(1-4)^2) =√(16+9)=5`.

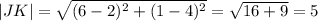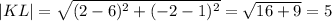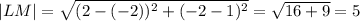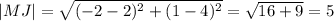Since all sides have the same lengths, you can state that this quadrilateral is rhombus.

Let's check whether quadrilateral JKLM is a square. To check this let find the lengths of diagonals:

`|JL|=√((2-2)^2+(-2-4)^2) =√(0+36)=6`,
`|MK|=√((-2-6)^2+(1-1)^2) =√(64+0)=8`.

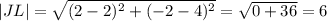
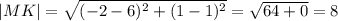
The lengths are different, so quadrilateral is not a square.

Answer: quadrilateral JKLM is a rhombus.