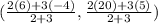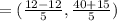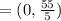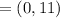Answer:
The coordinates of P are (0,11).
Explanation:
Since, when a point divides a line segment in the ratio of m : n that having endpoints
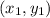 and
and
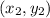 and lies between these points.
and lies between these points.
Then, the coordinates of the point are,

Hence, the coordinates of point P that divides the Line segment RW has endpoints R(-4,5) and W(6,20) in 2:3 ratio are,