Question

Samuel found the difference of polynomials {15x^2+11y^2+8x}-{7x^2+5y^2+2x}=_x^2+6y^2+6x

Answer 1

A = 8

Explanation:

Given : Samuel found the difference of two polynomial
`15x^2+11y^2+8x\\\\ 7x^2+5y^2+2x\\\\ \text{as}\ Ax^2+6y^2+6x`

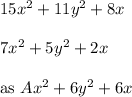
We have to find the value of missing coefficient A in the result so obtained.

Consider

`15x^2+11y^2+8x-\left(7x^2+5y^2+2x\right)`

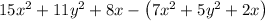
We first open parentheses as

`-\left(7x^2+5y^2+2x\right)=-\left(7x^2\right)-\left(5y^2\right)-\left(2x\right)`

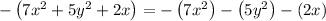
Apply plus - minus rule,
`+\left(-a\right)=-a`

`=-7x^2-5y^2-2x`

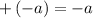
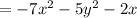
We get,

`=15x^2+11y^2+8x-7x^2-5y^2-2x`

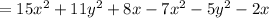
Grouping like terms, we have,

`=15x^2-7x^2+8x-2x+11y^2-5y^2`

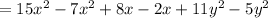
Simplify, we get,

`=8x^2+6x+6y^2`

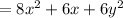
On comparing with Given result , we have A = 8

Answer 2

x^2*(15 -7) = 8x^2

The missing coefficient is 8.