Correct Answer:Option A. 17.1 Yards
Solution:Let the height of trapezium is x yards. According to the given data, we can express the lengths of bases in terms of height.
The short base is 3 yards greater than the height, so measure of short base will be (x+3) yards.
The longer base is 5 yards greater than the height, so measure of longer base will be (x+5) yards.
Area of trapezium is given to be 360 square yards.
Area of trapezium = 0.5 x (Height) x (Sum of Bases)
Using the values, we get:
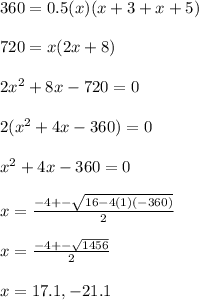
Since the height cannot have a negative value, we conclude that the height of trapezium rounded to nearest tenth of a yard will be 17.1 yards.