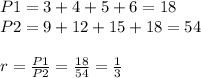Question

The sides of a polygon are 3, 5, 4, and 6. The shortest side of a similar polygon is 9. Find the ratio of their perimeters.

1/4
1/3
2/3
4/9

Answer 1

The answer is
`(1)/(3)`

Explanation:

In order to determine the answer we have to know about similar polygons.

Any two polygons are similar if their corresponding angles are congruent and the measures of their corresponding sides are proportional.

So, if two sides are proportional, where "a" is the lenght of the first polygon and "b" is the lenght of the second polygon, the ratio of these sides is:

`(a)/(b)=k`

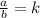
k is a rational number.

Applying the proportionality:

First polygon: its sides:

3

4

5

6

Second polygon: its sides:

9

x

y

z

These polygons are similar, so

`(9)/(3)=k\\ k=3`

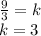
So, "x","y" and "z" values are:

`(x)/(4) =k=3\\x=4*3\\x=12\\\\(y)/(5)=k=3\\y=5*3\\y=15\\\\(z)/(6)=k=3\\z=6*3\\z=18`

Finally, the perimeter is the sum of the sides of the polygon, so the ratio of their perimeters is:

P1=Perimeter first polygon

P2=Perimeter second polygon

r=Ratio of their perimeters

`P1=3+4+5+6=18\\P2=9+12+15+18=54\\\\r=(P1)/(P2)=(18)/(54)=(1)/(3)`

Answer 2

The given polygon has a perimeter of 3 + 5 + 4 + 6 = 18
A similar polygon has sides that are 3 times as big ot 9 + 15 + 12 + 18 = 54

The ratio is 18/54 or 1/3