Question

If the mass of a radioactive substance is 8 grams and it has a half-life of 4 hours, how much mass remains after 8 hours?

Answer 1

The sample will lose half of its mass after 4 hours. The half life.
82=4
The sample will lose half of the remaining four after another half life.
42=2 Hope this helps! :)

Answer 2

Answer: 2 grams will be remaining.

Explanation: Half life is the time in which the amount of radioactive substance remains half.

For example if half life of a radioactive substance is 3 hours and we have 16 grams of it then in two hours, 8 grams will be remaining. In next two hours, 4 grams will be remaining. Similarly, in next two hours, 2 grams and further in next two hours 1 gram of the substance will be remaining.

For the given problem, the half life of the radioactive substance is 4 hours. It means the initial amount of this substance will remain half in 4 hours.

Originally we have 8 grams of the radioactive substance. In first 4 hours, 4 grams of the substance will be remaining. Now, in next 4 hours that is in total 8 hours, 2 grams of the substance will be remaining.

These problems could also be solved mathematically using the formula:

`(N)/(N_0)=(0.5)^n`

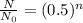
where,
`N_0` is the initial amount of the substance, N is remaining amount and n is the number of half lives.

number of half lives(n) =
`(time)/(half life)`

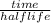
From given information, time is 8 hours and half life is 4 hours.

So, n =
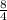`(8)/(4)` = 2

Initial amount is given as 8 grams and it asks to calculate the remaining amount. Let's plug in the values in the equation:

`(N)/(8)=(0.5)^2`

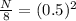
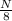`(N)/(8)` = 0.25

N = 8(0.25)

N = 2

So, from both ways 2 grams of the radioactive substance will be remaining after 8 hours.