First, we are going to find the common ratio of our geometric sequence using the formula:
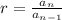
. For our sequence, we can infer that
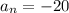
and
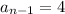
. So lets replace those values in our formula:
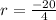
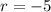
Now that we have the common ratio, lets find the explicit formula of our sequence. To do that we are going to use the formula:
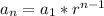
. We know that
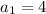
; we also know for our previous calculation that
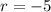
. So lets replace those values in our formula:
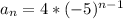
Finally, to find the 9th therm in our sequence, we just need to replace

with 9 in our explicit formula:
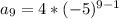
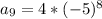
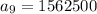
We can conclude that the 9th term in our geometric sequence is
1,562,500