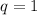Question

The quadratic equation x^2 + 8x + 15 = 0 can be rewritten as the equation below, where p and q are constants.

(x - p)^2 = q
What is the value of p?

Answer 1

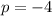`p = -4` and
`q = 1`

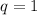
Explanation:

Given

`x^2 + 8x + 15 = 0`

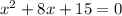
Required

Rewrite as:

`(x - p)^2 =q`

`x^2 + 8x + 15 = 0`

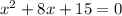
Subtract 15 from both sides

`x^2 + 8x + 15 - 15 = 0 - 15`

`x^2 + 8x = - 15`

-----------------------------------------------------------------------

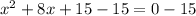
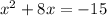
To make the equation a perfect square, follow these steps

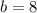`b = 8` ---- the coefficient of x

Divide both sides by 2:

`(b)/(2) = (8)/(2)`

`(b)/(2) = 4`

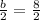
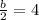
Square both sides

`((b)/(2))^2 = 4^2`

`((b)/(2))^2 = 16`

---------------------------------------------------------------------------------------

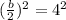
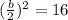
So, we add 16 t0 both sides of:
`x^2 + 8x = - 15`

`x^2 + 8x + 16 = - 15 + 16`

`x^2 + 8x + 16 = 1`

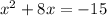
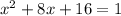
Factorize:

`x^2 + 4x + 4x+ 16 = 1`

`x(x + 4) + 4(x + 4) = 1`

`(x + 4) (x + 4) = 1`

`(x + 4)^2 = 1`

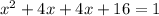
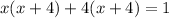
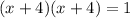
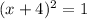
By comparison to:
`(x - p)^2 =q`

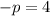`-p = 4` and
`q = 1`

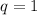
So, we have:

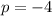`p = -4` and
`q = 1`