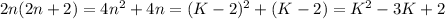Question

How to find a product of two consecutive even integers whose sum is a number?

Answer 1

Any even integer takes the form
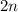
`2n`, where
`n` is any integer. Even integers occur every two integers following some even integer. This means the next even integer will take the form
`2n+2`.

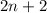
So you want to find
`2n(2n+2)=4n^2+4n`.

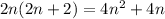
If you're told that the two integers add to some number, call it
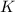
`K`, then we also know


`2n+(2n+2)=4n+2=K`

and from that we can solve for
`n`, which is exactly what we need to know in order to get a concrete value for the product above. In particular,


`4n+2=K\implies n=\frac{K-2}4`

and so


`2n(2n+2)=4n^2+4n=(K-2)^2+(K-2)=K^2-3K+2`