Answer:
A linear pair is two angles that are adjacent to each other and forms a line.
Supplementary Angle: If any two angles form a linear pair, then they are supplementary(i.e, 180 degree).
From the given figure,
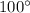 and
and
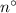 forms a linear pair.
forms a linear pair.
Also, if the two angles are linear pair, then they are supplementary angle.
then,
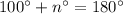
Simplify:
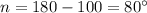
Vertical opposite angle theorems states about the two angles that are opposite to each other and are equal also.
From the figure,
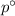 and
and
 are vertical opposite angle.
are vertical opposite angle.
therefore,
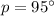
Now, to find the value of m;
Sum of the measures of the interior angles of a polygon with 4 sides is 360. degree.
here,
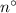 ,
,
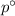 ,
,
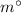 and
and
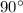 forms a qudrilateral.
forms a qudrilateral.
therefore, by definition:
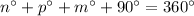
Substituting the values of
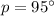 and
and
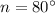 we have;
we have;
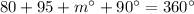 or
or
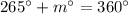
Simplify:

Therefore, the value of
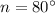 ,
,
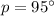 and
and
