Answer:
18.0625 feet
Explanation:
Given : The pear had a speed of 34 feet per second.
To Find: Approximately how far up in the tree was the pear before it fell?
Solution:
We are given that assume that the acceleration due to gravity is 32 feet per second squared
Formula =
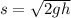
Where s is the speed , g is the acceleration due to gravity and h is the height
So,
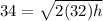
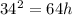
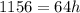
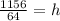
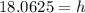
Hence the pear was at height of 18.0625 feet before it fell.