Question

Briana invested $12,500 into a fund that is expected to grow by 5.25% per year. How long with it take the fund to be worth $25,000? Round to the nearest year.

A) 2 years
B) 12 years
C) 14 years
D) 10 years

Answer 1

The answer is C) 14 years.
Plug it in to check:
12500(1+0.0525)^14
12500(2.05) = 25,587.01 (rounded to 25000)

Answer 2

14 years

Explanation:

Principal = $12,500

Rate = 5.35%

Amount = $25,000

Now we are supposed to find the time

Formula :
`A =P(1+(r)/(n))^(nt)`

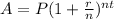
Where A = amount = $25,000

P = principal = $12,500

r = rate of interest in decimal = 0.0525

n = no. of compounds per year = 1

Substitute the values :

`25000 =12500(1+(0.0525)/(1))^(t)`

`25000 =12500(1.0525)^(t)`

`(25000)/(12500) =(1.0525)^(t)`

`2=(1.0525)^(t)`

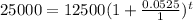
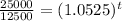
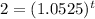
Taking log both sides

`\log 2 = t \log(1.0525)`

`(\log 2)/(\log 1.0525) = t`

`13.5464 = t`

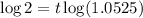
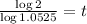
So, t = 13.5464 years ≈ 14 years

Thus it will take 14 years for the fund to be worth $25,000.