Question

Graph y = 3x to the second power - 5 and its inverse

Answer 1

You can see graph of the function
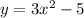
`y=3 x^(2) -5` in the first picture. Now to find its inverse, we are going to switch
`x` and
`y` in our function, and then solve for
`y`

`y=3 x^(2) -5`

`x=3y^(2) -5`

`x+5=3y^(2)`

`y^(2)= (x+5)/(3)`

`y=+or- \sqrt{ (x+5)/(3) }`
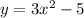
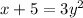
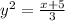
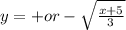
Remember that every time that you take a square root, you will have tow results: one positive and one negative. Therefore, our function
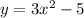
`y=3 x^(2) -5` will have tow inverses:
`y= \sqrt{ (x+5)/(3) }` and
`y=- \sqrt{ (x+5)/(3) }`.
In the first picture you can see the graph of the original function; in the second one the graphs of its inverses, and in the third one all the graphs together. Notice that our original function is a quadratic function, and quadratic functions don't have inverse functions unless their domains are restricted.