Question

Use the Babylonian method to estimate √103 to the nearest hundredth (show work!!! gave 26 pts)

Answer 1

Remember that the Babylonian method for finding square roots is divided in three steps:
Step 1:
- Make a reasonable guest. Since
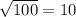
`√(100) =10`, our guest is that
`√(103) =10`.
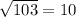
- Divide the original number by your guess. So,
`(103)/(10) =10.3`.
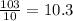
- Find the average of those numbers. So,

`(10+10.3)/(2)`

`(20.3)/(2)`

`10.15`
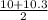
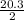
- Use that number as your next guess.

Step 2: Repeat step 1, but using the average, 10.15, as your next guess:
-
`(103)/(10.15) =10.14778325`
-
`(10+10.14778325)/(2)`

`(20.14778325)/(2)`

`10.07389163`

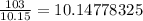
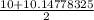
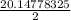
Step 3: repeat the process one last time, but using the average, 10.07389163, as your next guess:
-
`(103)/(10.07389163) =10.22444987`
-
`(10+10.22444987)/(2)`

`(20.22444987)/(2)`

`10.11222494`

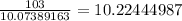
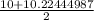
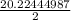
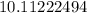
We can conclude that
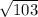
`√(103)`, using the Babylonian method, is equal to 10.11222494