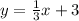Answer:
equation of the parallel line will be
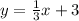 .
.
Explanation:
If the two lines have been given as y = mx + c
and y = m'x + c'
Where m and m' are the slopes of the given lines.
If these lines are parallel to each other then slopes of the lines will be same (m = m').
Equation of the given line is y =
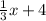 with he slope =
with he slope =
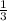
Then slope of a line parallel to this line m =
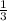
Equation of the parallel line will be
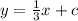
Since the line passes through a point (6, 5)
Then
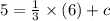
5 = 2 + c
c = 5 - 2
c = 3
Therefore, equation of the parallel line will be