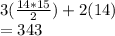Answer:
343
Explanation:
WE are to evaluate the sum of
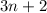 from n=1 to 14
from n=1 to 14
Symbolically this can be reprsented as
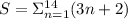
Splitting this into two separate terms we have
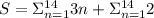
Since in I term 3 is a constant 3 can be taken out and similarly for II term if 2 taken out it becomes sum of 1, 14 times
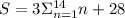
The first term is sum of 14 natural numbers and we use the formula
Sum =