Question

In ∆ABC with m∠C = 90° the sides satisfy the ratio BC:AC:AB = 4:3:5. If the side with middle length is 12 cm, find: 1) The perimeter of ∆ABC; 2) The area of ∆ABC; 3) The height to the hypotenuse.

Answer 1

6

Explanation:

6666666666666666666666666666666666666666666666

Answer 2

We are given the ratio as BC:AC:AB = 4:3:5

Middle side is AC and its measure is 12 cm.

Total ratio = 4+3+5 = 12

So that means :

`(3x)/(12)=12`

x=48

So perimeter =48 cm

Now let us find the other two sides: AB and BC

BC = 4x/ 12 = (4*48)/12= 16 cm

AB = 5x/12 (5*48)/12 =20 cm

Figure shows the actual representation of the triangle.

Area:

Area of triangle is given as :

`Area = (1)/(2) * base * height`

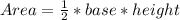
here base is 16 cm and height is 12 cm, plugging in formula,

`Area = (1)/(2) * 16 * 12`

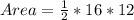
Area = 96 square cm

Height of Hypotenuse = AB = 20cm