Answer:
False; you would have more permutations than combinations.
Explanation:
The formula for taking combinations of n objects taken r at a time is
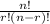
The formula for taking permutations of n objects taken r at a time is
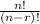
Comparing these two, we can see that the difference between the formulas is that the formula for combinations is divided by an extra r!. Since it is divided by a larger number, it will result in a smaller answer; therefore permutations give more results than combinations.