Question

A perfect square trinomial can be represented by a square model with equivalent length and width. Which polynomial can be represented by a perfect square model?

a. x2 – 6x + 9
b. x2 – 2x + 4
c. x2 + 5x + 10
d. x2 + 4x + 16

Answer 1

a. x2 – 6x + 9

Explanation:

In order to solve this you just have to try and factorize the options and the result should be two exact binomials. Remember that the formula for perfect square trinomial is:

`a^(2) +2ab+b^(2) =(a+b)(a+b)`

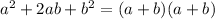
So we only have to factorize x2-6x+9=

As you can see, a is equal to X, and b equals 3:

(x-3)(x-3)=x2-6x+9

SO this is a perfect square trinomial.

Answer 2

The correct answer is

`A) x^2 - 6x + 9`

In fact, this is a trinomial of the form
`ax^2-bx+c`, whose solutions are given by

`x_(1,2)= (-b\pm √(b^2 -4ac) )/(2a)`
Using this formula for the trinomial of the problem, we find:

`x1,2= (6 \pm √(6^2-4\cdot 1\cdot 9))/(2) =3`
we see that this trinomial has two coincident solutions (x=3 with multiplicity 2). This means that it can be rewritten as a perfect square, in the following form:

`(x-3)^2`