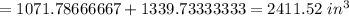Question

The figure is made up of a hemisphere and a cone.

What is the exact volume of the figure.



Enter your answer in the box.
in3

Answer 1

Answer:
`2411.52\ in^3`

Explanation:

In the given figure, we have a hemisphere and cone with same radius = 8 in.

The volume of hemisphere is given by :-

`\text{Volume}=(2)/(3)\pi r^3\\\\\Rightarrow\text{Volume}=(2)/(3)(3.14)(8)^3\\\\\Rightarrow\text{Volume}=1071.78666667\ in^3`

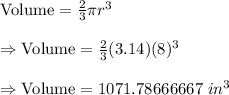
For cone, the height of cone = 20 in.

The volume of cone is given by :-

`\text{Volume}=(1)/(3)\pi r^2h\\\\\Rightarrow\text{Volume}=(1)/(3)(3.14)(8)^2(20)\\\\\Rightarrow\text{Volume}=1339.73333333\ in^3`

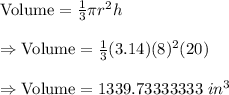
Now, the exact volume of the figure

=Volume of cone+Volume of hemisphere

`=1071.78666667+1339.73333333=2411.52\ in^3`

Answer 2

Volume of the figure = 2413.71 cubic inches.

Explanation:

Volume of the figure = Volume of the hemisphere + Volume of the cone

=
`(2)/(3) \pi r^(3) +(1)/(3) \pi r^(2) h`

`=(1)/(3) \pi r^(2) (2r + h)`

`=(1)/(3) ((22)/(7) )(8)(8)(16+20)`

`=(22(8)(8)(12))/(7)`

= 2413.71 cubic inches.