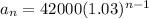Question

The starting salary at a company is $42,000 per year. The company automatically gives a raise of 3% per year. Write a recursive definition for the geometric sequence formed by the salary increase?

Answer 1

The recursive definition for the geometric sequence of salaries with a 3% annual raise begins with the first term of $42,000 and each subsequent term is obtained by multiplying the preceding term by 1.03.

Step-by-step explanation:

To write a recursive definition for the geometric sequence of salaries, we start by identifying the first term and the common ratio. The first term, denoted as a1, is the starting salary of $42,000. Each subsequent term is found by multiplying the previous term by the common ratio, which is 1 plus the 3% raise, or 1.03. Thus, we can write the sequence as follows:

• a1 = $42,000 (the starting salary)
• an = an-1 × 1.03 (for n ≥ 2, where an is the salary in the nth year and an-1 is the salary in the previous year)

This recursive formula describes the pattern of salary increases each year by applying the 3% raise.

Answer 2

To solve this, we are going to use the recursive formula for a geometric sequence:
`a_(n)=a_(1)r^(n-1)`
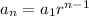
where

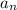
`a_(n)` is the nth term of the geometric sequence.

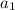
`a_(1)` is the first term of the geometric sequence.

`r` is the common ratio

`n` is the position of the term in the sequence.

We know that the starting salary is $42,000, so
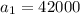
`a_(1)=42000`. Now, to find the common ratio
`r`, we need to find the next term in the sequence first:
We know from our problem that the company automatically gives a raise of 3% per year, so the next term in the sequence will be 42000 + 3%(42000) = 42000 + 1260 = 43260. Remember that the common ratio is the current term of the geometric sequence divided by the previous term of the sequence; we know that our current term is 43260 and the previous term is 42000, so:

`r= (43260)/(42000)`

`r=1.03`
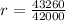
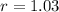
Now we can plug the values in our recursive formula:

`a_(n)=a_(1)r^(n-1)`

`a_(n)=42000(1.03)^(n-1)`

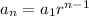
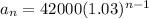
We can conclude that the recursive definition for the geometric sequence formed by the salary increase is:
`a_(n)=42000(1.03)^(n-1)`