Answer : D
The same amount of principal is invested in different accounts earning the same interest rate.
The account will not grow without interest
Lets assume , initial amount P= 100, rate of interest = 5%=>r= 0.05 and
number of years, t= 1
Calculate the simple interest
A = P + P*r*t = 100 + 100*.05*1= 105
In simple interest, $100 invested , amount earned = $105
Now we calculate earning interest compounded annually
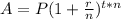
Lets assume , initial amount P= 100, rate of interest = 5%=>r= 0.05 and
number of years, t= 1, for compounded annually n= 1
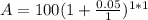 = 105
= 105
For interest compounded annually, $100 invested , amount earned = $105
Now we calculate earning interest compounded daily
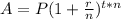
Lets assume , initial amount P= 100, rate of interest = 5%=>r= 0.05 and
number of years, t= 1, for compounded annually n= 365
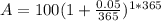 = 105.26
= 105.26
For interest compounded daily, $100 invested , amount earned = $105.26
So, An account compounded daily will have greatest accumulated value at the end of one year