Question

The volume (in cubic feet) of a room is represented by 12z3−27z12z3−27z. find expressions that could represent the remaining dimensions of the room when the length (in feet) is represented by 2z−32z−3.

Answer 1

The correct answers are:

3z and 2z+3.

Step-by-step explanation:

Volume is found by multiplying length, width and height. To use the volume and length to find the width and height, we would work backward and divide:


`(12z^3-27z)/(2z-3)`

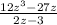
We can factor to work this division out.

In the numerator, we find the GCF first. Both terms are divisible by 3 and z, so we factor out 3z. When we do this, we divide both terms by 3z to finish the numerator:
12z³/3z = 4z²;
-27z/3z = 9

This gives us:

`(3z(4z^2-9))/(2z-3)`

4z²-9 is the difference of squares; using this to factor, we have:

`(3z(2z-3)(2z+3))/(2z-3)`

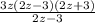
We have 2z-3 in both the numerator and denominator, so it will cancel out. This leaves us:

3z(2z+3)

This means one of the factors, 3z, is one dimension, and the other factor, 2z+3, is the other dimension.

Answer 2

The volume of a room = length * width * height
=12z³-27z
And by the analysis:
The volume = 12z³-27z
= ( 3z ) ( 4z²-9 ) ⇒ by taking (3z) common
= ( 3z )( 2z+3 )( 2z-3 ) ⇒ the difference between two squares

So the dimensions of the room will be 3z , 2z+3 , 2z-3
---------------------------------------------------------------------------
I have attached tha problem