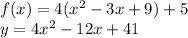Question

Find the quadratic function whose graph has a vertex at (3, 5) and passes through the point (1, -3). Express the function in both standard and general forms

Answer 1

Given vertex
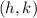
`(h,k)` the equation of the parabola is:

`f(x)=a(x-h)^2+k`.
Our vertex is the point
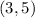
`(3,5)` so the equation is:

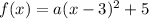
`f(x)=a(x-3)^2+5`. It remains to find a. We will use the point (1,-3) like
this:
Substitute x=1 and f(1)=-3 in the equation above we get the equation:

`-3=a(1-3)+5\\-3=-2a+5\\-2a=-8\\a=4`
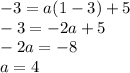
Equation of the parabola then:
`f(x)=4(x-3)^2+5`.
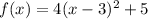
Expand in order to get the general form:

`f(x)=4(x^2-3x+9)+5\\y=4x^2-12x+41`