To solve this problem we will use the cosine rule. Formula is:
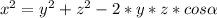
On left side we have side that we want to find length of. On right side we have other two sides and angle opposite to searched side.
We are given:
angle g=30°
g = 3
k = 4
In case of our formula we know x and y, but we do not know z. Now we have:
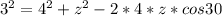
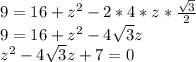
Now we solve this for z:

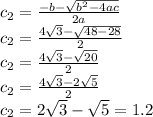
Our solution is A.