Question

How can you tell when a quadratic equation has no real solutions?

A. When the radicand is negative

B. When b in the quadratic formula is greater than the radicand

C. When the radicand equals zero

D. When the radicand is not a perfect square

Answer 1

The answer above is correct.

Explanation:

I got it right on the quiz

Answer 2

Answer: The correct option is (A). When the radicand is negative

Step-by-step explanation: We are given to select the correct option by which we can tell that a quadratic equation has no real solutions.

We know that for the quadratic equation

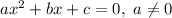`ax^2+bx+c=0,~a\\eq 0` the radicand is given by

`D=b^2-4ac.`

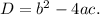
Based on the radicand "D", we have the following rules:

(i) If D > 0 (positive), then the two solutions are real and unequal.

(ii) If D = 0, then the two solutions are equal.

(iii) If D< 0 (negative), then the two solutions are complex (not real).

Thus, when the radicand is negative, then the quadratic equation has no real solutions.

Option (A) is correct.