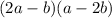Question

Factor completely, then place the factors in the proper location on the grid. 2a2 + 2b2 - 5ab

Answer 1

Factored form is (2a-b)(a-2b).

Step-by-step explanation:
To factor this, we can first write it as 2a²-5ab+2b².

We want factors of 2a²(2b²)=4a²b² that sum to -5ab. -4ab(-1ab) = 4a²b², and -4ab+-1ab = -5ab, so that is what we will use. This is how we will "split up" the middle term:
2a²-4ab-1ab+2b².

We group together the first two terms and the last two terms:
(2a²-4ab)+(-1ab+2b²).

Factor out the GCF of each group. The GCF of the first group is 2a: 2a(a-2b). The GCF of the second group is -1b: -1b(a-2b).

These two now have another common factor, (a-2b). We factor this out and get our answer, (a-2b)(2a-b).

Answer 2

For this case we have the following expression:

`2a ^ 2 + 2b ^ 2 - 5ab`
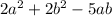
Rewriting the expression we have:

`2a ^ 2 - 5ab + 2b ^ 2`
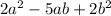
From here, we factor the expression completely.
We have then:

`(2a - b) (a - 2b)`
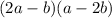
Let's check the factorization.
To do this, we multiply the terms within the parenthesis.
We have then:

`2a ^ 2 - 4ab - ab + 2b ^ 2`
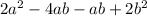
Rewriting:

`2a ^ 2 - 5ab + 2b ^ 2`
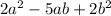
Therefore, the factorization is correct.
Answer:

`(2a - b) (a - 2b)`