Question

Please help me understand this

Answer 1

QS bisects <PQT so <PQS = <SQT
m<SQT = 8x - 25
m<PQT = 9x + 34
m<PQT = 2(m<SQT)
9x + 34 = 2(8x - 25)
9x + 34 = 16x - 50
7x = 84
x = 12

m<SQT = 8(12) - 25 = 71

m<PQS = m<SQT = 71

m<PQT = 2(m<PQS) = 2(71) = 142

m<TQR = m<SQR - m<SQT = 112 - 71 = 41

answer
x = 12
m<PQS = 71
m<PQT = 142
m<TQR = 41

Answer 2

The value of x is 12.

The measure of ∠PQS is 71°.

The measure of ∠PQT is 142°.

The measure of ∠TQR is 41°.

Explanation:

Given information: QS bisects ∠PQT, m∠SQT=(8x-25)°, m∠PQT=(9x+34)° and m∠SQR=112°.

QS bisects ∠PQT it means QS divides ∠PQT in two equal parts.

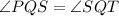`\angle PQS=\angle SQT` .... (1)

`\angle SQT=(1)/(2)(\angle PQT)`

`2\angle SQT=\angle PQT`

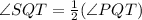
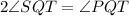
Substitute the value of each angle.

`2(8x-25)=(9x+34)`

`16x-50=9x+34`

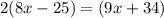
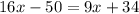
Isolate variable terms.

`16x-9x=50+34`

`7x=84`

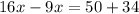
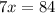
Divide both sides by 7.

`x=12`

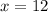
The value of x is 12.

From equation (1) we get

`\angle PQS=\angle SQT=(8x-25)^(\circ)`

`\angle PQS=(8(12)-25)^(\circ)`

`\angle PQS=71^(\circ)`

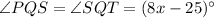
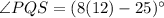
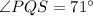
The measure of ∠PQS is 71°.

`m∠PQT=(9x+34)^(\circ)`

`m∠PQT=(9(12)+34)^(\circ)`

`m∠PQT=142^(\circ)`

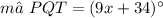
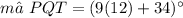
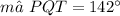
The measure of ∠PQT is 142°.

`m∠TQR=m\angle SQR-m\angle SQT`

`m∠TQR=112^(\circ)-71^(\circ)`

`m∠TQR=41^(\circ)`

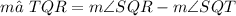
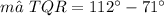
The measure of ∠TQR is 41°.