Answer:
The correct option is D.
Explanation:
The endpoints of the diameter of a circle are (9, 4) and (5, 2).
The midpoint of these end points is circle.
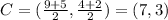
The center of the circle is (7,3).
The length of diameter is

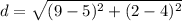
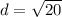
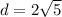
The radius of the circle is
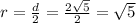
The general equation of the circle is
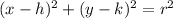
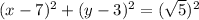
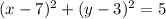
Therefore correct option is D.