Question

A rectangular stirp of asphalt paving is 5 meters longer than it is wide. its area is 300 square meters. find the length and width

Answer 1

20 m and 15 m

Explanation:

Let the width of the rectangle is x.

According to the question, the length is 5 m more than the width.

So, the length of the rectangle is x + 5.

Area of the rectangle is given by

`A = length * widthA = x * (x+5)A = x^(2)+5x`

As given in the question area is 300 square metre

So,
`x^(2)+5x = 300`

`x^(2) + 5x -300 = 0`

`x^(2) + 20 x - 15x - 300 = 0`

`x(x + 20) -15 (x + 20) = 0`

`(x + 20) (x - 15) = 0`

`x = - 20, 15`

The width cannot be negative.

So width is equal to 15 m and length is equal to ( 15 + 5) = 20 m .

Answer 2

Let's call L the width of the rectangle and W its width. The area of the rectangle is the product between the length and the width, and we are also told that the area is 300 square meters, so we can write

`A=L\cdot W=300`
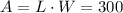
Moreover, we know that the length is 5 meters longer than the width:

`L=W+5`
We have a system of 2 equations in 2 unknown variables, L and W. If we substitute the second equation into the first one, we get

`(W+5)\cdot W=300`

`W^2+5W-300=0`
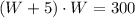
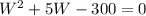
which has two solutions: W=-20 and W=15. We can discard the negative solution since it does not have physical meaning, and now we can substitute the value of W into the second equation to find L:

`L=W+5=15+5=20`
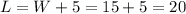Therefore, the rectangle has width 15 meters and length 20 meters.