Question

Solve the equation.

3x^2 + 12 = 0

Answer 1

`\quad \huge \quad \quad \boxed{ \tt \:Answer }`

`\qquad \tt \rightarrow \:x = 2i`

____________________________________

`\large \tt Solution \: :`

`\qquad\displaystyle \tt \rightarrow \: 3 {x}^(2) + 12 = 0`

`\qquad\displaystyle \tt \rightarrow \: 3{x}^(2) = - 12`

`\qquad\displaystyle \tt \rightarrow \: {x}^(2) = - (12)/(3)`

`\qquad\displaystyle \tt \rightarrow \: x {}^(2) = - 4`

`\qquad\displaystyle \tt \rightarrow \: x = √( - 4)`

`\qquad\displaystyle \tt \rightarrow \: x = √( (- 1)(4))`

`\qquad\displaystyle \tt \rightarrow \: x = √( - 1) \sdot √(4)`

`\qquad\displaystyle \tt \rightarrow \: x = i \sdot2`

`\qquad\displaystyle \tt \rightarrow \: x = 2i`

[ i represents iota, i² = -1, (complex number) ]

Answered by : ❝ AǫᴜᴀWɪᴢ ❞

Answer 2

`x=2i`

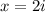
Explanation:

Given equation:

`3x^2+12=0`

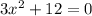
Factor 3 from the left side of the equation:

`\implies 3(x^2+4)=0`

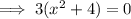
Divide both sides of the equation by 3:

`\implies(3(x^2+4))/(3)=(0)/(3)`

`\implies x^2+4=0`

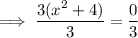
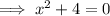
Subtract 4 from both sides:

`\implies x^2+4-4=0-4`

`\implies x^2=-4`

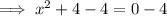
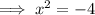
Square root both sides:

`\implies √(x^2)=√(-4)`

`\implies x^2=√(-4)`

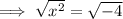
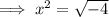
Rewrite -4 as 2² · -1:

`\implies x=√(2^2 \cdot-1)`

`\textsf{Apply radical rule} \quad √(ab)=√(a)√(b):`

`\implies x=√(2^2)√(-1)`

`\textsf{Apply radical rule} \quad √(a^2)=a, \quad a \geq 0:`

`\implies x=2√(-1)`

`\textsf{Since $√(-1)=i$}`

`\implies x=2i`

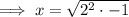
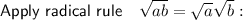
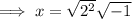
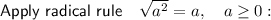
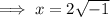
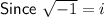
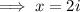
Imaginary numbers

Since there is no real number that squares to produce -1, the number
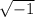`√(-1)` is called an imaginary number, and is represented using the letter i.

An imaginary number is written in the form
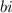`bi`, where
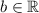`b \in \mathbb{R}`.