Question

If an atomic nucleus were the size of a dime how far away might one of its electrons be?

Answer 1

The radius of a nucleus of hydrogen is approximately
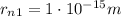
`r_(n1)=1\cdot 10^(-15)m`, while we can use the Borh radius as the distance of an electron from the nucleus in a hydrogen atom:
`r_(e1)=5.3 \cdot 10^(-11)m`

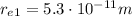
The radius of a dime is approximately
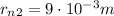
`r_(n2) = 9\cdot 10^(-3)m`: if we assume that the radius of the nucleus is exactly this value, then we can find how far is the electron by using the proportion

`r_(n1):r_(e1)=r_(n2):r_(e2)`
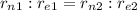
from which we find

`r_(e2)= (r_(e1) r_(n2))/(r_(n1))= ((5.3 \cdot 10^(-11)m)(9\cdot 10^(-3)m))/(1 \cdot 10^(-15)m)=477 m`

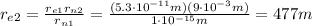
So, if the nucleus had the size of a dime, we would find the electron approximately 500 meters away.