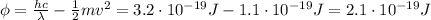Question

Electrons are ejected from a metallic surface with speeds ranging up to 4.9 105 m/s when light with a wavelength of λ = 625 nm is used. (a) what is the work function of the surface?

Answer 1

In the photoelectric effect, part of the energy of the photon (E=hf) of the incoming light is used to extract the photoelectron from the metal (work function:
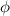
`\phi`) and part is given to the electron as kinetic energy:
`K= (1)/(2)mv^2`:

`hf = \phi + (1)/(2)mv^2`
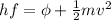
The frequency of the photon is related to the wavelenght:
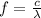
`f= (c)/(\lambda)`, and so we can re-write the formula as

`\phi = (hc)/(\lambda) - (1)/(2) mv^2`
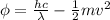
where:

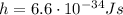
`h=6.6 \cdot 10^(-34)Js` is the Planck constant

`c=3 \cdot 10^8 m/s` is the speed of light

`\lambda = 625 nm = 625 \cdot 10^(-9)m` is the wavelength of the light

`m=9.1 \cdot 10^(-31)kg` is the electron mass

`v= 4.9 \cdot 10^5 m/s` is the electron speed.

Substituting these numbers into the equation, we can find the work function of the surface:

`\phi = (hc)/(\lambda)- (1)/(2)mv^2=3.2 \cdot 10^(-19)J-1.1\cdot 10^(-19)J=2.1 \cdot 10^(-19)J`