Answer:
The mass expelled will be 116.239 kg
Step-by-step explanation:
We have given the mass of the rocket M = 3180 kg
Initial velocity of the rocket v= 115 m /sec
Now change in velocity

From the conservation of momentum change in momentum is equal to the momentum of gas expelled
Let the mass expelled is m
We have also given that speed of the gas expelled
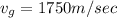
So
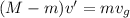

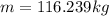
So the mass expelled will be 116.239 kg