Question

Which of the following represents the line of symmetry of the parabola represented by the equation x2 - 10x + 21 = 0?

A.x = 3
B.x = 2
C.x = 4
D.x = 5

Answer 1

the correct answer is 5

Answer 2

Let us first define line of symmetry of parabola :

It is the line of symmetry of a parabola that divides a parabola into two equal halves that are reflections of each other about the line of symmetry. It intersects a parabola at its vertex. It is a vertical line with the equation of x = -b/2a.

So using the formula x=-b/2a, we can find the line of symmetry of parabola here.

We are given the equation:

`x^(2) -10x+21 =0`

If we compare it with the quadratic equation :

`ax^(2) +bx+c=0`

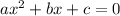
we get a=1, b=-10 and c=21

Now plugging the values of a and b in the formula x=-b/2a,

`x= (-b)/(2a)`

`x= (-(-10))/(2(1))`

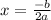
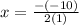
x=5

So the line of symmetry of given parabola is given by x=5

Option D is correct answer.