Question

Quadrilateral BCDE is inscribed inside a circle as shown below. Write a proof showing that angles C and E are supplementary. Circle A is shown with an inscribed quadrilateral labeled BCDE.

Answer 1

The sum of angle C and E is 180°. So, C and E are supplementary angles.

Explanation:

Given information: Quadrilateral BCDE is inscribed inside a circle.

To prove : angles C and E are supplementary, i.e., ∠C+∠E=180°.

Proof:

BCDE is a cyclic quadrilateral.

According to central angles theorem, the inscribed angle on a circle is half of its central angle.

By using Central angle theorem

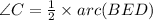
`\angle C=(1)/(2)* arc (BED)`

`2\angle C=arc (BED)` .... (1)

`\angle E=(1)/(2)* arc (BCD)`

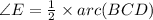
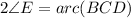`2\angle E=arc (BCD)` ..... (2)

The complete central angles of a circle is 360°.

`arc (BED)+arc (BCD)=360^(\circ)`

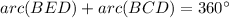
Using (1) and (2), we get

`2\angle C+2\angle E=360^(\circ)`

`2(\angle C+\angle E)=360^(\circ)`

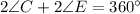
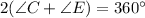
Divide both sides by 2.

`\angle C+\angle E=180^(\circ)`

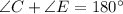
The sum of angle C and E is 180°. So, C and E are supplementary angles.

Hence proved.