Question:
What is the sum of the arithmetic sequence 18 E t=1 (5t-4)
Answer & Step-by-step explanation:
We have to find the sum of Arithmetic series from t = 1 to t = 18 represented by (5t - 4)
The formula to find the sum of an Arithmetic series when first and the last term is known is:
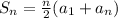
n = Total number of terms = 18
 = First Term = 5(1) - 4 = 1
= First Term = 5(1) - 4 = 1
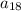 = 18th Term = 5(18) - 4 = 86
= 18th Term = 5(18) - 4 = 86
Using the values in the above formula, we get:
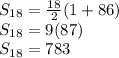
Thus, the sum of 18 terms of the given Arithmetic Series is 783.