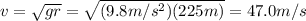Question

A car drives on a circular track with a constant speed of 84 m/s. The track has a radius of 225 m. a. What is the centripetal acceleration of the car? (1 point) b. What is the acceleration of the car measured in g? (1 point) c. What speed would give the car an acceleration of 9.8 m/s2? (1 point)

Answer 1

a.
`31.4 m/s^2`

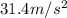
The centripetal acceleration is given by

`a=(v^2)/(r)`

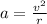
where

v is the speed

r is the radius

In this problem,

v = 84 m/s

r = 225 m

So the centripetal acceleration is

`a=((84 m/s)^2)/(225 m)=31.4 m/s^2`

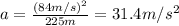
b. 3.2 g

The value of g is

`g=9.8 m/s^2`

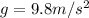
So, the acceleration of the car measured in g is

`a = (31.4 m/s^2)/(9.8 m/s^2)=3.2 g`

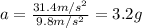
c. 47.0 m/s

In order to have an acceleration of

`a=g=9.8 m/s^2`

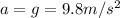
The car should have a speed v such that the centripetal acceleration is equal to this value:

`g=(v^2)/(r)`

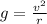
Solving the equation for v, we find

`v=√(gr)=√((9.8 m/s^2)(225 m))=47.0 m/s`