Consider, pls, this option:
1. if a required line has a form y=ax+b, then points A(-1;6); B(6;k) and C(20;3) belong to it.
2. According to the item 1 it is possible to make up the system of equations for A and C:
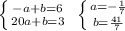
Knowing, that a=-1/7 and b=41/7, it is possible to write the equation of required line:
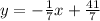
3. Using coordinates of point B:
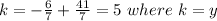
Answer: 5.