Question

Factor to find the zeros of the function defined by the quadratic expression. 9x2 − 63x − 702

Answer 1

The zeros of the quadratic expression are: x=-6 and x=13

Explanation:

First we need to use the common factor:

`9x^2-63x-702=9(x^2-7x-78)`

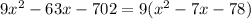
Now factorizing the expression of the parentheses we have:

`9(x^2-7x-78)=9(x+6)(x-13)`

To know the zeros we need to equal to zero the expression then:

`9(x+6)(x-13)=0`

`(x+6)(x-13)=0`

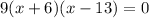
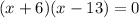
This expression will be zero when x=-6 or when x=13.

Answer 2

Not that it will help all that much, but you could take out 9 as a common factor.
9(x^2 - 7x - 78) = 0 so since 9 but itself can't produce a zero, we can divide by 9
x^2 - 7x - 78 = 0
There are 3 factors of 78
2 13 and 3
6 and 13 differ by 7 (6 comes from putting the 2 and 3 together by multiplying.
(x - 13)(x + 6) = 0

x -13 =0
x = 13

x + 6 = 0
x = - 6

The two zeros are (-6,0) and (13,0)