Question

solve by completing the square: A rectangular patio has a length of x+6m, a width of x+8m, and the total area of 400 m^2. find the dimensions to the nearest tenth

Answer 1

`(x + 8)( x + 6) = 400 \\ x { }^(2) + 14x - 352 = 0 \\ (x + 7) {}^(2) - 401 = 0 \\ x = - 7 + √(401) \\`

Answer 2

Length of the rectangular patio = (x + 6) m

width of the rectangular patio = (x +8)m

Area of rectangle=Length*Width.

400=(x+6)(x+8)

400=
`x^(2)`+14x+48

For completing square, first add - 48 on both side

400 - 48 =
`x^(2)`+14x

352 =
`x^(2)`+14x

To make a complete square add the third term =
`\left ( (-b)/(2a) \right )^{}2`

a= 1 and b= 14

Third term =
`\left ( (-14)/(2) \right )^{}2`

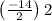
Third term = 49

Now add 49 in both side of the equation

352 + 49 =
`x^(2)`+14x + 49

401 =
`\left ( x+7 \right )^(2)`

Taking square root on both sides

`x + 7 = \pm √(401)`

We can not consider the negative value

so x + 7 = 20.02

x = 20.02 -7

x= 13.02

Length of the rectangular patio = (x + 6) = 13.02 + 6 = 19.02 m

width of the rectangular patio = (x +8) = 13.02 + 8 = 21.02 m