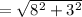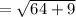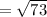Question

Given that P = (5, 9) and Q = (13, 12), find the component form and magnitude of vector PQ.

Answer 1

`\bf \begin{cases} P=(5,9)\\ Q=(13,12) \end{cases}\qquad\stackrel{\vec{PQ}}{\ \textless \ 13-5~~,~~12-9\ \textgreater \ }\implies \ \textless \ 8~,~3\ \textgreater \`

Answer 2

ANSWER

The vector in the component form is


`\binom{8}{3}`
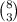
and the magnitude is


`√(73)`


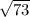
Step-by-step explanation

The given points are P=(5,9) and Q=(13,12).


We want to find the component form of vector PQ.

Let the components of vector PQ be


`\binom{x}{y}`

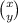
Vector PQ can express in terms of position vectors as follows:




This implies that;



`\binom{x}{y} =\binom{13}{12} - \binom{5}{9}`

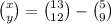
We subtract the corresponding components to get;


`\binom{x}{y} = \binom{13 - 5}{12 - 9}`
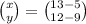
The vector in component form is


`\binom{x}{y} = \binom{8}{3}`



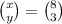
The magnitude of vector PQ is


`= \sqrt{ {x}^(2) + {y}^(2) }`




`= \sqrt{ {8}^(2) + {3}^(2) }`



`= √(64+ 9)`





`= √(73)`